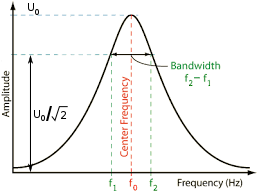
Bandwidth
For a fixed forcing function of magnitude \( F \), a relative maximum amplitude \( U_0 \) of the system occurs at the resonant frequency \( f_0 \). The amplitude is lower on either side of the resonant frequency. On the low side of the resonant frequency \( f_0 \) there is a frequency \( f_1 \) where the amplitude is only \( U_0 / \sqrt{2} \). Similarly, on the high side of the resonant frequency \( f_0 \) there is a frequency \( f_2 \) where the amplitude is only \( U_0 / \sqrt{2} \). Frequencies \( f_1 \) and \( f_2 \) are called the half-power frequencies (i.e., the frequencies where the power will have dropped by half compared to the power at \( f_0 \) at maximum amplitude \( U_0 \)).
The bandwidth Bw (in Hz) is defined as:
\begin{align} \label{eq:11801a} Bw = f_2 - f_1 \end{align}
|
|
|
The bandwidth is related to the Q (quality factor) by —
\begin{align} \label{eq:11802a} Q = \frac{f_0}{Bw} \end{align}
Hence, a narrow bandwidth indicates a high Q.
Notes:
- A complex system (such as an ultrasonic stack) may have many resonances. A separate bandwidth (and associated Q) can be determined for each resonance.
- For a system that includes piezoelectric ceramics, the amplitude curve of figure 1 becomes more complicated because of the electro-mechanical effect of the ceramics.
Also see —
Attenuation
Damping ratio
Log decrement
Loss tangent